No.376 立方体のN等分 (2)
レベル : / 実行時間制限 : 1ケース 5.000秒 / メモリ制限
: 512 MB / 標準ジャッジ問題
タグ : / 解いたユーザー数 110
作問者 :
tails
/ テスター :
紙ぺーぱー
タグ : / 解いたユーザー数 110
作問者 :
tails
/ テスター :
紙ぺーぱー
問題文最終更新日: 2016-06-05 01:30:50
問題文
立方体を何枚かの平面で切断して $N$ 個の合同な直方体に分割しようとしています。
このような分割をするためには、立方体を何枚の平面で切断すればいいでしょうか？
平面の枚数 $T$ の取り得る最小値 $Tmin$ および最大値 $Tmax$ を答えてください。
なお、立方体の切断片を移動したりせずに、全体が元の立方体の形と位置を保ったまま
$T$ 枚の平面で切断するものとします。
※「立方体のN等分 (1)」とは入力の制約だけが異なります。
入力
$N$
$1 \lt N \lt 10^{14}$
$N$ は整数です。
立方体を $N$ 個の合同な直方体に分割します。
出力
$Tmin$ $Tmax$
平面の枚数の最小値 $Tmin$ および最大値 $Tmax$ を出力してください。
$Tmin$ と $Tmax$ の間はスペースを1つ空けてください。
最後に改行してください。
サンプル
サンプル1
入力
12
出力
4 11
下図に赤で示すように、4枚の平面で切断して12個の合同な直方体に分割することができます。
これより少ない枚数で分割することはできませんので、 $Tmin = 4$ になります。
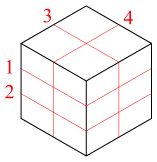
また、底面に平行な11枚の平面で切断して12個の合同な直方体に分割することができます。
これより多い枚数で分割することはできませんので、 $Tmax = 11$ になります。
サンプル2
入力
13
出力
12 12
どのように切断しても12枚の平面で切断することになりますので、 $Tmin = Tmax = 12$ です。
提出するには、Twitter 、GitHub、 Googleもしくは右上の雲マークをクリックしてアカウントを作成してください。