問題文

$N$ 頂点 $0$ 辺の重み付き無向グラフ $G$ と 変数 $X$ があります。グラフの頂点にはそれぞれ $0$ から $N-1$ までの番号付けがされています。
変数 $X$ ははじめ $ X_{0} $で初期化されています。
グラフ $G$ における2頂点間 $u$, $v$ の距離 ${\rm dist} (u, v) $ を次のように定義します。
$$ {\rm dist} (u, v) = 頂点\ u\ から頂点\ v\ へのパスに含まれる辺すべての重みの最大値の最小値 $$ 同一頂点での距離は ${\rm dist}(v, v) = 0$ とします。
以下のような $Q$ 個のクエリが与えられるので、グラフ $G$ と変数 $X$ に対して順に処理してください。

• 1 v w：頂点 $v$ と頂点 $X$ を重み $w$ の辺で結ぶ。入力順について $w$ が広義単調増加となっていることが保証される。
• 2 u v：頂点 $u$ と頂点 $v$ が連結でない場合-1を出力する。連結である場合、${\rm dist} (u, v) $ を出力し、 $X$ に ${\rm dist} (u, v) $ を加算する。
  その後、$X$ を $N$ で割ったあまりとする。
• 3 v：頂点 $v$ と同一の連結成分に含まれるすべての頂点対についての距離の総和を $998244353$ で割ったあまりを出力する。
  すなわち、頂点 $v$ と連結である頂点 (頂点 $v$ も含む)が $K$ 個あるとし、それぞれ $ u = (u_{1}, u_{2}, u_{3}, \cdots, u_{K})$ とした際の $$ \left( \sum_{i=2}^{K}\sum_{j=1}^{i-1} {\rm dist}(u_{i}, u_{j}) \right) \bmod\ 998244353 $$ を出力する。頂点 $v$ と連結である頂点が $1$ つしかない (頂点 $v$ のみである) 場合、0 を出力する。
• 4 value：$X$ に値 ${\rm value}$ を加算する。その後、$X$ を $N$ で割ったあまりとする。

入力

$N\ X_{0}\ Q$
${\rm Query}_{1}$
${\rm Query}_{2}$
${\rm Query}_{3}$
$\ \ \ \ \vdots$
${\rm Query}_{i}$
$\ \ \ \ \vdots$
${\rm Query}_{Q}$

• $1 \leq N \leq 2 \times 10^{5}$
• $1 \leq Q \leq 3 \times 10^{5}$
• $0 \leq X_{0} < N$
• ${\rm Query}_{i}$について
  
  タイプ1のクエリのとき

  $1\ v_{i}\ w_{i}$

  タイプ2のクエリのとき

  $2\ u_{i}\ v_{i}$

  タイプ3のクエリのとき

  $3\ v_{i}$

  タイプ4のクエリのとき

  $4\ {\rm value}_{i}$

  ・$0 \leq u_{i}, v_{i}, {\rm value}_{i} < N$
  ・$0 \leq w_{i} \leq 10^{9}$
  ・$i < j$ のとき $w_{i} \leq w_{j}$ を満たす。


• 入力はすべて整数

出力

タイプ2、タイプ3のクエリが合計で $K$ 個与えられるとして、 $i\ (1 \leq i \leq K)$ 行目にそれぞれのクエリの回答を1行に出力してください。最後に改行してください。

サンプル

サンプル1

入力

5 1 10
1 0 1
2 0 1
1 1 2
2 0 2
3 1
2 4 1
1 1 4
4 1
1 4 4
3 1

出力

1
2
5
-1
17

サンプル1の説明を見る (クリックで展開します)

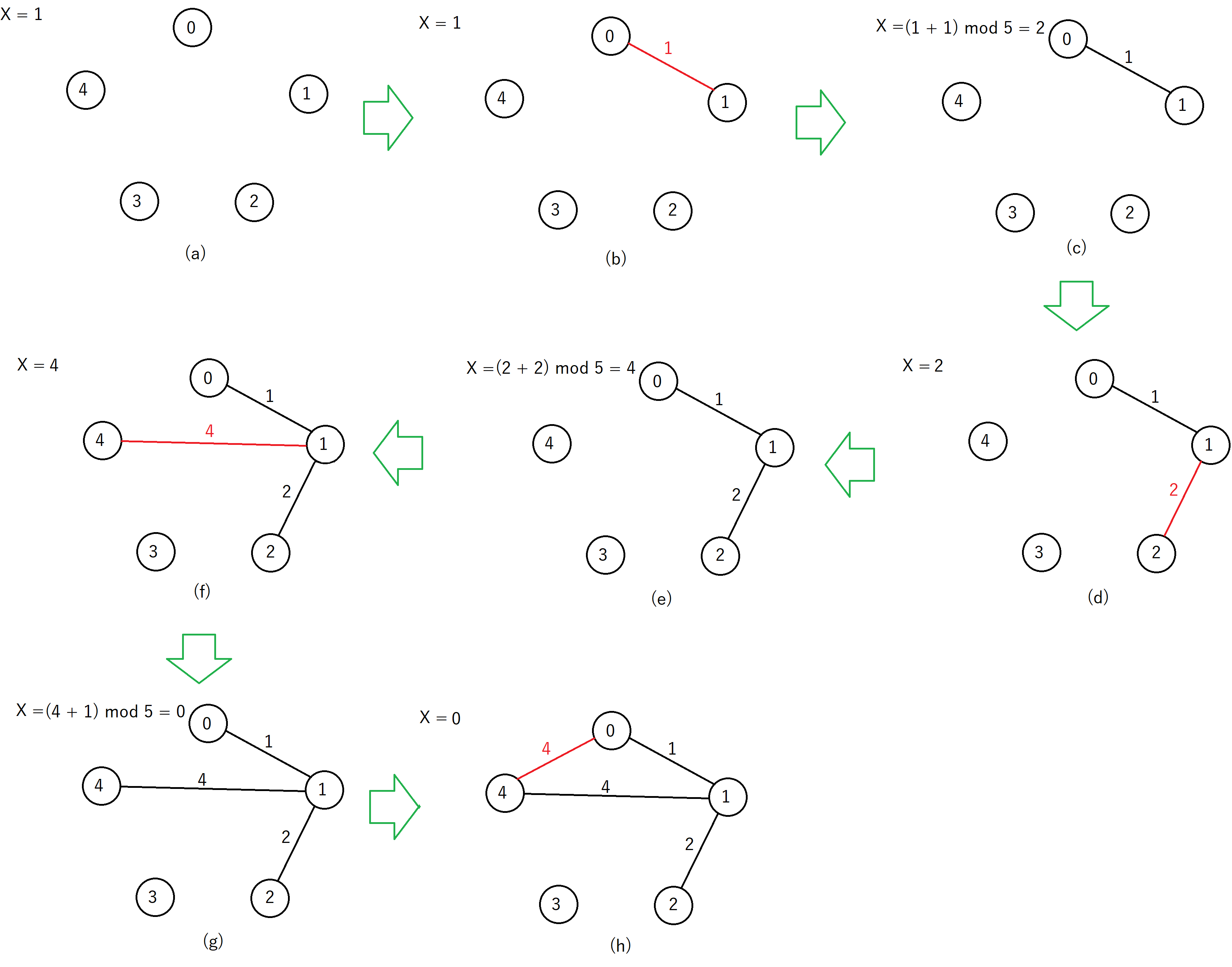
初期状態は $N$ 頂点 $0$ 辺となっていて変数は $X = 1$ に初期化されています。

• 1 0 1：1つ目のクエリでは、頂点 $0$ と頂点 $X = 1$ を重み $1$ の辺で結びます。(b)
• 2 0 1：2つ目のクエリでは、${\rm dist}(0, 1) = 1$ を出力します。これにより変数は $X = 1 + 1 = 2$ となります。(c)
• 1 1 2：3つ目のクエリでは、頂点 $1$ と頂点 $X = 2$ を重み $2$ の辺で結びます。(d)
• 2 0 2：4つ目のクエリでは、${\rm dist}(0, 2) = 2$ を出力します。これにより変数は $X = 2 + 2 = 4$ となります。(e)
• 3 1：5つ目のクエリでは、頂点 $1$ と同じ連結成分に属する頂点対の距離の総和を出力します。(e)
  ${\rm dist}(0, 1) = 1$、${\rm dist}(0, 2) = 2$、${\rm dist}(1, 2) = 2$ なのでこれらの総和である $5$ を出力します。
• 2 4 1：6つ目のクエリでは、${\rm dist}(4, 1)$ の出力が求められますが、非連結なため $-1$ を出力します。(e)
• 1 1 4：7つ目のクエリでは、頂点 $1$ と頂点 $X = 4$ を重み $4$ の辺で結びます。(f)
• 4 1：8つ目のクエリでは、変数 $X$ に $1$ を加算し、$N$ で割ったあまりとします。$ X = (4 + 1) \bmod 5 = 0$ となります。(g)
• 1 4 4：9つ目のクエリでは、頂点 $4$ と頂点 $X = 0$ を重み $4$ の辺で結びます。(h)
• 3 1：10個目のクエリでは、頂点 $1$ と同じ連結成分に属する頂点対の距離の総和を出力します。(h)
  ${\rm dist}(0, 1) = 1$、${\rm dist}(0, 2) = 2$、${\rm dist}(0, 4) = 4$、${\rm dist}(1, 2) = 2$、${\rm dist}(1, 4) = 4$、${\rm dist}(2, 4) = 4$なので $17$ を出力します。

10 2 12
1 0 14
2 0 2
1 2 22
1 1 28
1 7 94
2 4 6
3 8
1 5 126
1 3 212
1 6 223
1 9 245
3 6

14
-1
0
4135

4 2 11
1 3 91
1 0 111
2 1 0
3 2
2 0 1
1 1 210
1 2 230
3 1
2 3 3
2 0 3
2 1 2

-1
313
-1
943
0
111
210