No.479 頂点は要らない
問題文
maiさんは $n$ 個の頂点と $m$ 個の辺から成る無向グラフを持っている。
そのグラフの各頂点には $0$ から $n-1$ までの非負整数が重複なく割り当てられている。
また、 $j$ 番目の辺は、 $a_j$ と $b_j$ の頂点に接続している。
舞葉君がmaiさんから辺を買い取ろうと考えていたときに、maiさんから次のような提案をされた。
- 非負整数 $i$ が割り当てられている頂点の価格は $2^i$ 円である。
- 頂点を購入すると、その頂点に接続する辺がセットで付いてくる。
- 購入した頂点と辺は、maiさんのグラフから失われ、補充されることは無い。
- 辺のみを購入することは出来ない。
舞葉君は辺に飢えているので、maiさんが持っている辺を全て購入したい。
彼の富は無限なので、どれほど高額な頂点でも購入することができるが、なるべく安く抑えたいらしい。
舞葉君が支払うべき最小の金額を2進数で出力してください。
入力
$n$ $m$ $a_1$ $b_1$ $a_2$ $b_2$ ... $a_m$ $b_m$
$ 2 \le n \le 100000$
$\lceil n/2 \rceil \le m \le \min \{100000 ,n(n-1) / 2 \}$
$0 \le a_i \lt b_i \le n-1$
どの辺にも接続しないような頂点が存在するようなグラフは与えられない。
多重辺も存在しない($i \neq j$ならば$a_i \neq a_j$か$b_i \neq b_j$のいずれかを満たす)。
テストケースのファイル名に "s#{数字}" の形式で $n$ と $m$ の追加制約が記されていることがある。
対応する追加制約は以下の通りである。
- s12 : $n \le 12$を満たす
- s1000 : $n \le 1000$かつ$m \le 1000$を満たす
- s100000 : $n$または$m$が制約上限に極めて近い
出力
舞葉君が全ての辺を手に入れるために必要な支払うべき最小の金額を2進数で出力してください。
余分な0(例えば、0010など)は出力しないでください。
最後に改行してください。
サンプル
サンプル1
入力
4 5 0 1 0 2 0 3 1 2 2 3
出力
101
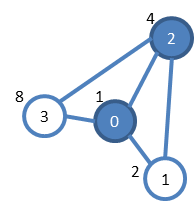
上の図は、標準入力から与えられるグラフです。頂点中央の数字は割り当てられた非負整数、頂点の左上の数字は価格です。
0と2を選ぶと全ての辺を手に入れることができ、5円で済みます。5は2進数で101なので、101を出力します。
0,1,3を選んでも全ての辺を手に入れることはできますが、11円掛かってしまいます。
サンプル2
入力
6 5 0 4 1 2 1 5 2 5 3 4
出力
1111
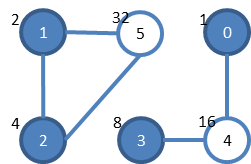
連結グラフとは限りません。
サンプル3
入力
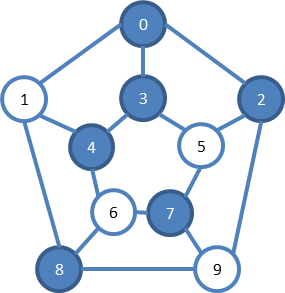
10 15 0 1 0 2 0 3 1 4 1 8 2 5 2 9 3 4 3 5 4 6 5 7 6 8 6 7 7 9 8 9
出力
110011101
提出するには、Twitter 、GitHub、 Googleもしくは右上の雲マークをクリックしてアカウントを作成してください。
