定義

3つの自然数から成る数列 $x = (x_1,x_2,x_3)$ が次の条件を満たす時，$x$ は門松列と呼びます．

1. $x_1,x_2,x_3$ は全て異なる
2. 3つの要素のうち $x_2$ が最も大きい，あるいは最も小さい

始点と終点が異なり，どの頂点も高々一度しか通らない，ある頂点からある頂点への行き方をパスと呼びます．
長さ2のパスとは，2つの辺と3つの頂点によって構成されているパスのことです．

さらに，この問題では，門松パスと呼ばれるものを定義します．
長さ2のパスの始点から終点までの頂点に書かれた数字を順に $x=(x_1,x_2,x_3)$ として， $x$ が門松列を満たすとき，そのパスを門松パスと呼びます．

問題文

$N$ と $M$ が与えられます．

次の条件を満たすグラフ(門松グラフ)が構築可能かどうか判定し，可能ならそのグラフを出力してください．

• 頂点数 $N$，辺の数 $M$
• 頂点 $i$ には 自然数 $a_i$ が書き込まれている．
• 辺$j$ は頂点 $u_j$ と頂点 $v_j$ に接続されている．
• グラフは連結であり，多重辺，ループ辺が存在しない．
• どの長さ2のパスを取り出しても門松パスになっている．

入力

$N$ $M$

$3 \le N \le 10^5$
$2 \le M \le 10^5$

自然数が与えられる．

出力

$S$
$a_1$ $\ldots$ $a_N$
$u_1$ $v_1$
$\ldots$
$u_M$ $v_M$

$S \in \{\text{YES},\text{NO}\}$
$1 \le a_i \le 10^5$
$1 \le u_j,v_j \le N$

数値を出力する場合，自然数を出力してください．
頂点は 1-indexed で表現してください．

制約を満たすグラフが構築不能であれば，1行目に"NO"と出力してください．

制約を満たすグラフが構築可能であれば，1行目に"YES"と出力し，2行目以降にグラフの情報を出力してください．

スペシャルジャッジです．条件を満たす出力は複数存在しますが，どれを出力しても正答となります．

サンプル

サンプル1

入力

6 6

出力

YES
5 1 4 2 3 4
1 2
2 3
3 4
1 4
1 5
1 6

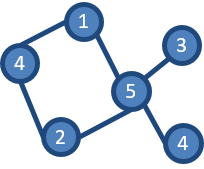
出力で示されているグラフを描いてみると，上の図になります．
どの長さ2のパスを取り出しても門松パスであることが確認できます．
よって，$N=6,M=6$ の条件を満たす門松グラフは存在しました．

10 8

NO

10 30

NO

7 8

YES 
1 2 3 4 5 6 7 
1 4
2 4
2 5
3 5
3 6
3 7
1 5
1 6