No.1166 NADA DNA
タグ : / 解いたユーザー数 26
作問者 :
 蜜蜂
/ テスター :
蜜蜂
/ テスター :
問題文
ナダ地方には $N$ 種類のサルが生息しています。
あなたは DNA 配列を用いてナダ地方のサルの系統樹を作成することになりました。
系統樹は生物の種間関係を示す全二分木で、葉ノードが生物に対応し、内部ノードが分岐点に対応しています。
DNA 配列は A, T, G, C からなる文字列で表され、サル種 $1$ からサル種 $N$ のそれぞれについて、長さ $L$ の DNA 配列 $G_1$ から $G_N$ が与えられます。
系統樹の不正確性の指標として「系統樹のコスト」が以下に説明されるように定義されます。
----
<系統樹のコスト>
まず次のように、$2$ 種類のサルの DNA 距離 ${\rm D}(X,\ Y)$ を定義します:相異なる $2$ 種類のサル種 $X, Y$ の DNA 配列 $G_X,\ G_Y$ について、$G_X$ と $G_Y$ のそれぞれ左から $i$ 番目 $(1\leq i\leq L)$ の文字が一致しなかった数(ハミング距離)をその $2$ 種の DNA 距離と定義し、${\rm D}(X,\ Y)$ と表すことにします。
例えば、$G_X,\ G_Y$ がそれぞれ ACGTTA, ACCTGA であるとき、左から $3, 5$ 番目の文字が異なっているため、${\rm D}(X, Y) = 2$ です。
次に、分岐点のコストを次のように定義します:分岐点の片側の二分木に属する種のうち一つを種 $A$ 、もう片側の二分木に属する種のうち一つを種 $B$ としたとき、${\rm D}(A,\ B)$ の最小値をその分岐点のコストとします。
系統樹の各分岐点のコストの和を「系統樹のコスト」とします。
----
あなたはなるべくコストの低い系統樹を作りたいです。$N$ 種類のサルの系統樹のコストとして考えられる最小の値を出力してください。
入力
$N\ \ \ L$
$G_1$
$G_2$
$\ \vdots$
$G_N$
$N,\ L$ は整数
$2\leq N\leq 1000$
$1\leq L\leq 50$
$G_i$ は A, T, G, C から成る長さ $L$ の文字列 $(1 \leq i \leq N)$
出力
答えを$1$行に出力してください。
最後に改行してください。
サンプル
サンプル1
入力
3 4
AAAA
AGGA
AGGT
出力
3
系統樹は $3$ パターン考えられます。
(A) の場合、種 $2$ と種 $3$ の分岐点のコストは ${\rm D}(2,\ 3)=1$ で、種 $1$ の分岐点のコストは ${\rm D}(1,\ 2)=2$ と ${\rm D}(1,\ 3)=3$ の $2$ つのうち最も小さい値である $2$ となります。よって(A)の系統樹のコストは $3$ です。
(B), (C) のコストはそれぞれ $4, 3$ となり、出力すべき最小値は $3$ です。

サンプル2
入力
4 7
TCAAGCT
TAACGCC
ACACGTT
ACGACTC
出力
10
系統樹は $15$ パターン考えられます。
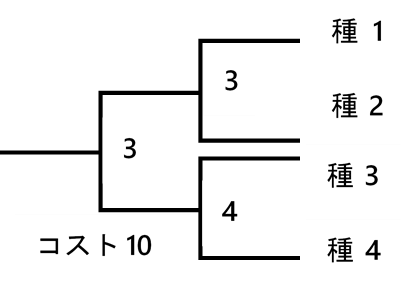
以下の系統樹の場合、種 $1$ と種 $2$ の分岐点のコストは ${\rm D}(1,\ 2)=3$ で、種 $3$ と種 $4$ のコストは ${\rm D}(3,\ 4)=4$ であり、一番系統樹の根に近い分岐点のコストは ${\rm D}(1,\ 3)=3,\ {\rm D}(1,\ 4)=5,\ {\rm D}(2,\ 3)=4,\ {\rm D}(2,\ 4)=6$ のうち最も小さい値である $3$ となります。よって以下の系統樹のコストは $10$ です。
コストが $9$ 以下の系統樹は存在しないので、出力すべき最小値は $10$ です。
出典
灘校75回生中学卒業記念コンテスト: NADA DNA
writer: tetanura
tester: Mitarushi
HackerRankの規約に基づいて移植しております。一部改変したところがあります。
提出するには、Twitter 、GitHub、 Googleもしくは右上の雲マークをクリックしてアカウントを作成してください。
